Project 2
Project Description
In this project, the goal is to have fun with filters and frequencies. The main operation I used is the gaussian convolution kernel. Through the gaussian filter, I am able to extract low frequencies from an image, which in turn enables me to also extract high frequencies from an image by subtracting the original image by its low frequencies. The low and high frequencies then lead to very interesting things, such as image sharpening (part 2.1), hybrid image (part 2.2), and image blending (parts 2.3 and 2.4).
Part 1.1 Finite Difference Operator
In this part, I am given two finite difference operators D_x and D_y, where D_x is a (1 * 2) matrix [1, -1] and D_y is a (2 * 1) matrix [1,-1]. By convolving the image with the finite difference operators, I found the partial derivatives in the x and y direction respectively. I then extracted the gradient magnitude image by taking the square root of the sum of the individual squares of the partial derivatives. To make an edge image, I binarized the gradient magnitude image with threshold = 0.28.

Original Image

D_x

D_y

Gradient Magnitude

Edge (threshold = 0.28)
Part 1.2 Derivative of Gaussian (DoG) Filter
Since the edge image result of convolving the cameraman image directly with the finite difference operators is weak, I implemented two convolutions. The first convolution is the same as part 1.1, and the second is convolving with a gaussian filter with kernel size = 10 and sigma = 2. As shown, the resulting edge image is much more prominent due to reduction in high frequency noise by convolving with the gaussian low frequency filter.
There are two methods in implementation. The first method is to implement the two convolutions separately. I first convolved the cameraman image with the gaussian filter, then I convolved the low frequency image with the finite difference operators. The second method is to generate the gaussian filter which is convolved with the finite difference operators before lastly convolving with the cameraman image. Both methods produce exactly the same result.
Two Convolutions

D_x

D_y

Gradient Magnitude

Edge (threshold = 0.28)

Gaussian D_x Filter

Gaussian D_y Filter
Single Convolution

D_x

D_y

Gradient Magnitude

Edge (threshold = 0.28)
Part 2.1 Image "Sharpening"
Image sharpening is done by adding some high frequency details of an image to the original image to “sharpen” it. In order to extract high frequencies, I first need to blur the original image, then subtract the blurred image from the original image. As a result of some mathematical simplification, image sharpening can be implemented as one single filter.
In the two examples below, it is obvious that both images are sharpened. In other words, more details are added to the original image. In the case of Taj, since the original image contains some noise, the sharpened Taj looks better. On the other hand, since the original image of the elephant already contains a lot of details, the sharpened effect is not as good visually.

Taj Original

Taj sharpened

Elephant Original

Elephant Sharpened
Part 2.2 Hybrid Images
A hybrid image is an image that changes according to viewing distance. It is made up by blending two different images together. The theory behind it is that humans perceive high frequency at a close distance and low frequency at a long distance.
My implementation involved four parts. First, I need to align two images. Second, I generated a separate gaussian filter for each image. Third, I pass each image to their associated gaussian filter to extract their low frequencies. For the image that I want to extract its high frequency, I subtract its low frequency from the original image. Lastly, I added the low frequency from one image and high frequency from the other image together and normalized.

Biden Original
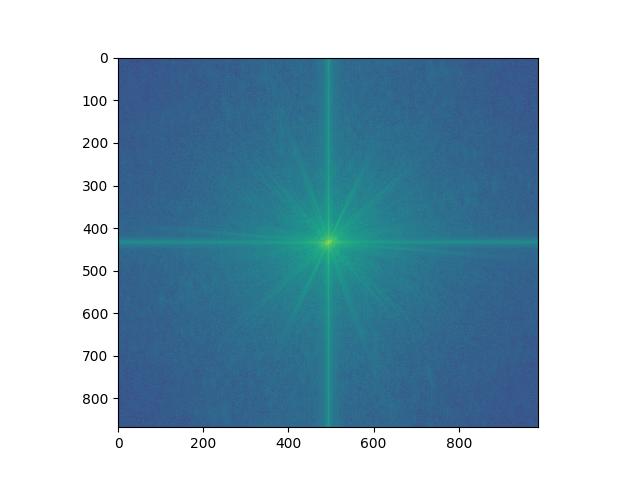
Log Magnitude FFT of Biden Original

Biden High Frequency
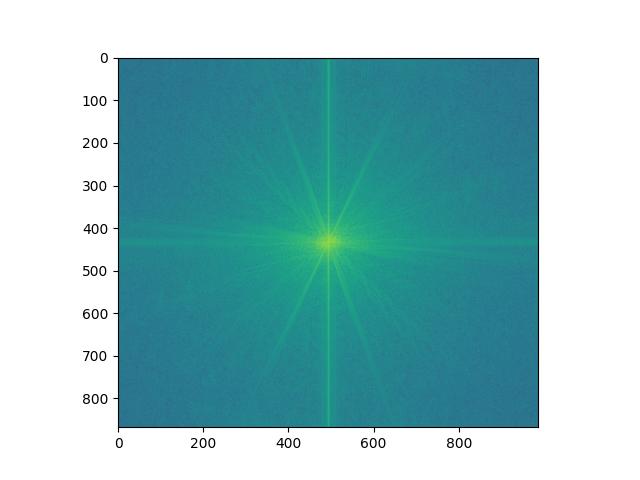
Log Magnitude FFT of Biden High Frequency

Harris Original
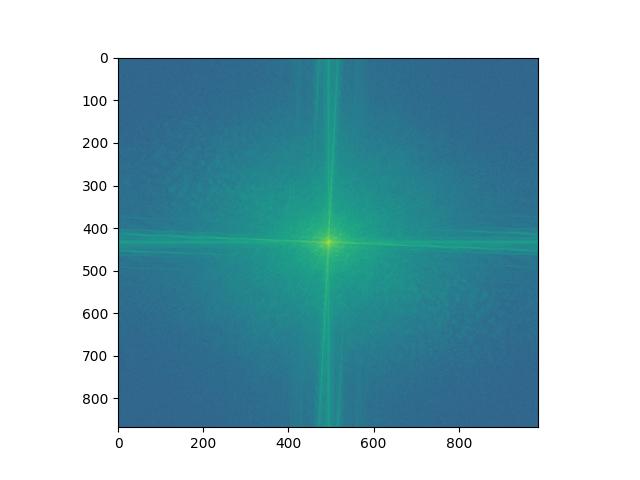
Log Magnitude FFT of Harris Original

Harris Low Frequency
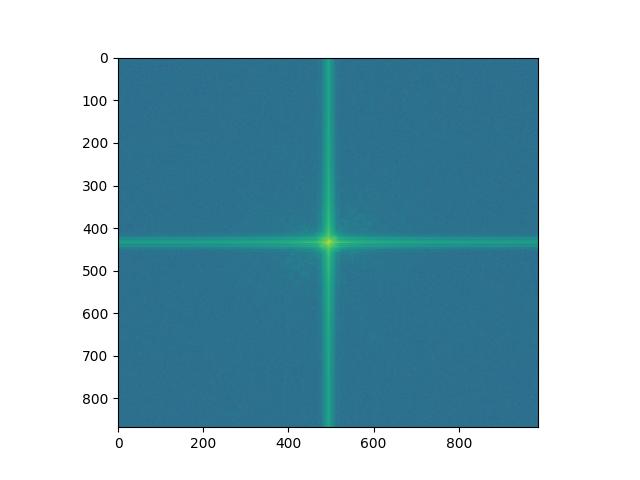
Log Magnitude FFT of Harris Low Frequency

Biden-Harris Hybrid
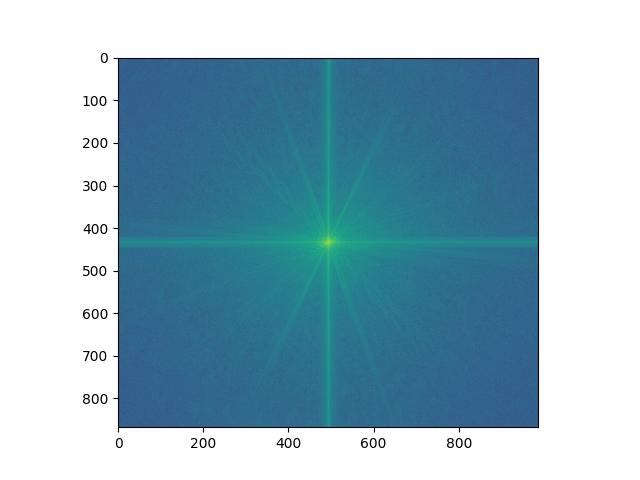
Log Magnitude FFT of Biden-Harris Hybrid

Trump 1 Original

Trump 2 Original

Trump 1 and Trump 2 Hybrid

Boat Original

Car Original

Boat-Car Hybrid
As shown above in my examples, the biden-harris hybrid performs pretty well because the two images are very similar to each other, which makes it easy to align. However, the boat-car in particular looks bad. The reason is that the middle of the boat contains almost no edges, which makes the car visible both from a close and long viewing distance.
Part 2.3 Gaussian and Laplacian Stacks
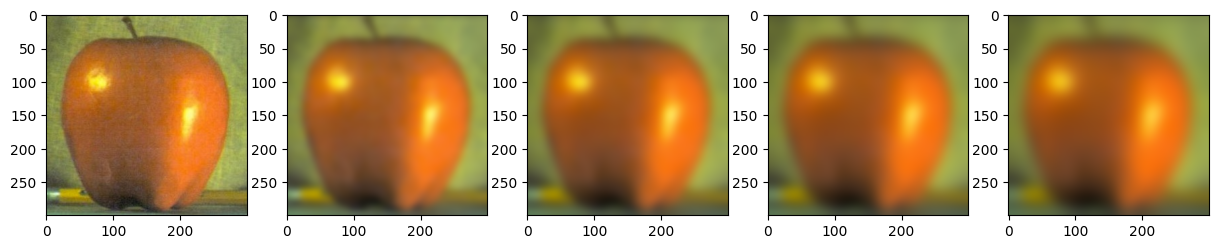
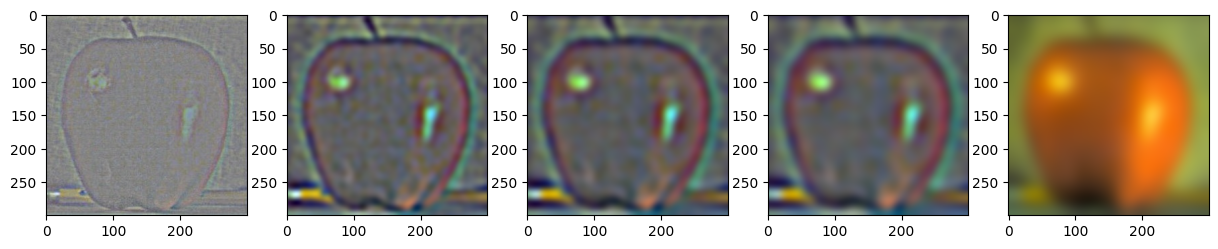
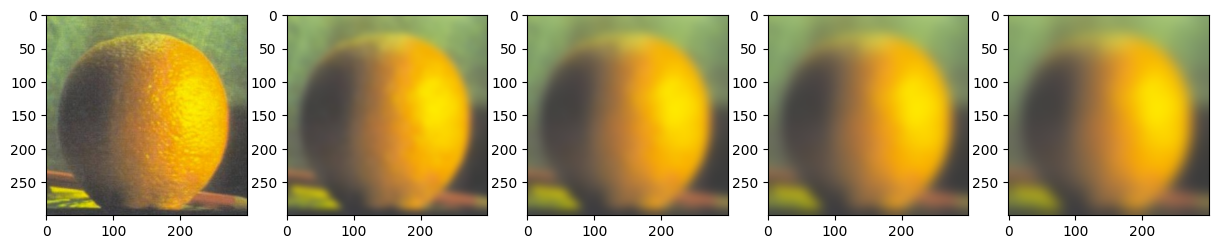
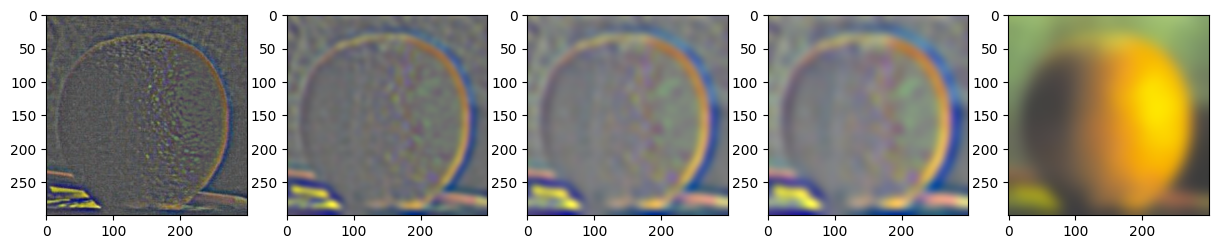
The gaussian and laplacian stacks are used for multiresolution blending in part 2.4. The gaussian stack is generated by repeatedly convolving an image with a gaussian filter. The laplacian stack is generated by subtractions between successive low frequency images in the gaussian stack.
Apple Gaussian Stack
Apple Laplacian Stack
Orange Gaussian Stack
Orange Laplacian Stack
Part 2.4 Multiresolution Blending
Following the generation of gaussian and laplacian stacks, a blended image can be constructed by starting from the last level of the laplacian stack, using a gaussian mask to do a weighted sum at each level, and adding together all blended images.
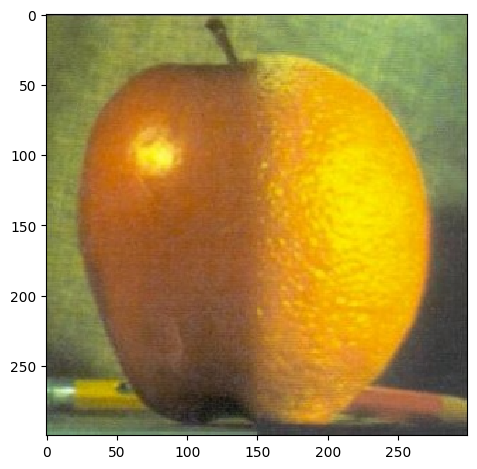
In my examples, the oracle uses a vertical mask, the desert-plane uses a horizontal mask, and the golden-gate-bridge-rocket uses an irregular mask which I generated from photoshop.
Oraple!